728x90
2011번: 암호코드
나올 수 있는 해석의 가짓수를 구하시오. 정답이 매우 클 수 있으므로, 1000000으로 나눈 나머지를 출력한다. 암호가 잘못되어 암호를 해석할 수 없는 경우에는 0을 출력한다.
www.acmicpc.net
DP개념을 사용하면 되지만, 나름 처리해야 하는 예외들이 몇 가지 있어서 3번째 제출에 맞췄다.
기본적으로 나는 2차원 배열을 이용해서
1. [n][0]에는 결합하지 못하고 그냥 붙는 경우
2. [n][1]에는 결합할 수 있어서 해석의 가짓수가 늘어나는 경우로 나눴다.
1)의 경우는 42 같은 경우이다. 42는 결합되지 못하고 db라는 해석 한 가지밖에 없다.
2)의 경우 26 같은 경우이다. 26은 bf와 z라는 해석 두 가지가 나온다.
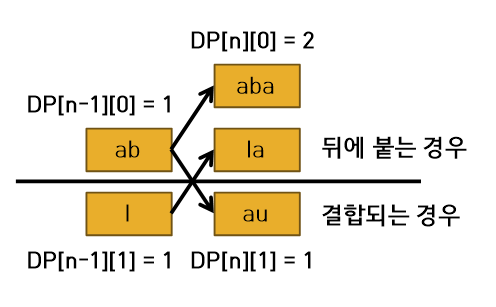
따라서 n번째 숫자가 결합이 가능하면 [n][0]에 n-1까지 저장한 가짓수를 더해주고, [n][1]에 추가로 결합되는 케이스를 더해준다.
즉, dp[n][0] = dp[n-1][0] + dp[n-1][1]
dp[n][1] = dp[n-1][0] 이다.
또한 n번째 숫자가 결합이 불가능하면 그냥 기존 케이스들에 단일 알파벳이 하나 붙는 경우이므로 [n][0]에 기존 케이스를 저장해준다. (증가 X)
즉, dp[n][0] = dp[n-1][0] + dp[n-1][1] 이다.

그리고 생각해야 할 케이스는
- 앞자리가 0인 경우
- 암호가 잘못되어 암호를 해석할 수 없는 경우에는 0을 출력한다.
1) 맨 앞자리에 0이 있으면 0을 출력한다.
2) 암호 도중에 0이 연속으로 등장하면 0을 출력한다. - 앞자리가 1인 경우
그냥 결합이 가능한 점화식을 진행시켜준다. - 앞자리가 2인 경우
1) 다음 숫자가 7 이상이면 해당되는 알파벳이 없다.
- 결합이 불가능한 케이스로 생각
2) 다음 숫자가 0~6이면 결합이 가능하므로 결합이 가능한 점화식이 진행된다. - 앞자리가 3 이상인 경우
1) 3 이상은 결합이 불가능하므로 결합이 불가능한 케이스
즉, [n+1][0]에 그 전의 케이스들 [n][0] + [n][1]을 더해서 저장해준다.
(그냥 이제까지 케이스에 알파벳이 하나 붙는다고 생각하면 편하다. 증가되는 케이스가 없기 때문이다.)
코드는 정리가 되지 않아서 좀 지저분하다.
그냥 위의 케이스대로 논리를 진행하면 될 것이다.
#include <iostream>
using namespace std;
#define mod 1000000
int dp[5001][2];
string s;
int main() {
cin >> s;
dp[0][0] = 1;
int result = s.size()-1;
if (s[0] - '0' == 0) {
cout << 0;
return 0;
}
for (int i = 1; i < s.size(); i++) {
if (s[i - 1] - '0' <= 2) { // 결합 가능
if (s[i] - '0' == 0) {
dp[i][1] = (dp[i - 1][0]) % mod; // 0이면 결합만 생기므로 [1]으로 옮겨주기만 한다.
if (s[i - 1] - '0' == 0) {
cout << 0;
return 0;
}
}
else {
if (s[i - 1] - '0' == 2 && s[i] - '0' >= 7) { // 결합불가
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
}
else {
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % mod; // 기존 단어들에 새롭게 단어 추가
dp[i][1] = (dp[i - 1][0]) % mod;//([1]으로 갯수를 추가로 더해준다)
}
}
}
else {
if (s[i] - '0' == 0) { // 결합도 안되고 0에 해당되는 단어도 없다. 단어 생성 불가 50의 경우
cout << 0;
return 0;
}
else { // 아니면 기존의 단어들에 뒤에 붙기만 하므로 [0]에 더해준다.
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
}
}
}
cout << (dp[result][0] + dp[result][1]) % mod;
}
728x90
'문제 풀이 > 백준 알고리즘' 카테고리의 다른 글
| [baekjoon 2110] 공유기 설치 (이진탐색) (C++) (0) | 2021.02.07 |
|---|---|
| [baekjoon 11725] 트리의 부모 찾기- 트리, 그래프, BFS, DFS (C++) (0) | 2021.02.05 |
| [baekjoon 2225] 합분해- DP(동적 프로그래밍) (C++) (0) | 2021.02.02 |
| [baekjoon 11052] 카드 구매하기- DP(동적 프로그래밍) (C++) (0) | 2021.01.28 |
| [baekjoon 11054] 가장 긴 바이토닉 부분 수열- DP(동적 프로그래밍) (C++) (0) | 2021.01.27 |
![[baekjoon 2011] 암호코드- DP(동적 프로그래밍) (C++)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FVWyed%2FbtqVJQU6RtX%2FzBrEUf01dRxlg4HAXnujw1%2Fimg.png)